生物電極脫氮工藝的在線模糊控制研究(二)
彭永臻 王淑瑩 周利 (哈爾濱建筑大學市政環境工程學院)
黑田正和 許燕青 (日本群馬大學工學部)
摘 要 系統地介紹了生物電極脫氮法模糊控制器的設計及其計算機算法,其中包括輸入變量模糊化處理和輸出變量非模糊化處理的計算方法、模糊控制規則的建立、模糊控制的計算機算法及其程序框圖等。設計的在線模糊控制器具有結構簡單、可靠、穩定、可行性好、對進水硝酸態氮負荷變化的適應性強、有利于避免過量投加有機物并盡可能節省運行費用等優點。
關鍵詞 污水處理 生物電極法 脫氮 模糊控制
模糊控制器的設計包括:確立模糊化和非模糊化處理的計算方法,設計模糊控制器的控制規則,編制模糊控制計算機算法的應用軟件,合理選擇模糊控制算法的采樣時間等。其中模糊控制規則又是模糊控制器設計的關鍵,利用語言歸納手動控制策略的過程,實際上就是建立模糊控制器控制規則的過程。在此以前,還要選擇描述輸入輸出變量的詞集和定義各模糊變量的模糊子集。顯然,本模糊控制器的設計應當結合生物電極脫氮法本身的工藝特點來展開。
1 模糊控制器的設計
1.1 模糊控制器輸入變量的模糊化
由模糊控制原理可知[1、3],模糊控制器的輸入和輸出變量都是確定量,而模糊控制算法本身要求模糊變量。這就需要首先將精確的輸入變量經模糊化處理變為模糊變量。
將文獻[1]中式(2)的連續確定量Noff的偏差E[1]化為在[-6,+6]之間變化的離散整型變量xe,如表1所示。
| xe | -6 | -5 | -4 | -3 | -2 | -1 | -0 |
| E(mg/l) | -∞~-1 | -1~0.8 | -0.8~-0.6 | -0.6~-0.4 | -0.4~-0.2 | -0.2~-0.02 | -0.02~0 |
| xe | +0 | +1 | +2 | +3 | +4 | +5 | +6 |
| E(mg/l) | 0~0.02 | 0.02~0.2 | 0.2~0.4 | 0.4~0.6 | 0.6~0.8 | 0.8~1.0 | 1.0~+∞ |
連續確定量偏差E的變化量CE也可作同樣處理,化為在[-6,+6]之間變化的離散整型變量yce。區間[-6,+6]上的離散整數稱作模糊變量的規格化論域。其CE的變化范圍(即基本論域)應通過試驗和實際運行經驗來確定,它與傳感器精度、測定速度和采樣時間等有關。
由于模糊控制器的控制規則表現為一組模糊條件語句,在條件語句中通常用7或8個表示大、中、小的模糊語言變量來描述輸入輸出變量大小,如
NB=Negative Big(負大)
NM=Negative Midium(負中)
NS=Negative Small(負小)
NO=Negative Zero(負零)
或者用
O=Zero(零)
PO=Positive Zero(正零)
PS=Positive Small(正小)
PM=Positive Midium(正中)
PB=Positive Big(正大)
模糊變量必須用隸屬函數來表示。其具體函數關系取決于被控制系統本身的特性,但一般用正態函數來描述隸屬函數μ是合適的,如下:
μ(x)=exp[-((x-b)/δ)2]
式中 b——參數,隸屬函數的隸屬度為1時x的值
δ——隸屬函數的范圍
δ的大小直接影響隸屬函數曲線的形狀,而隸屬函數的形狀不同會導致不同的控制特性,圖1給出了用隸屬函數曲線表示論域X中元素x對某一模糊變量A的隸屬程度μ。
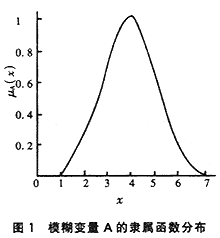
通常,選用的8個模糊變量的隸屬函數可用下式表示:
設0<x1<x2<x3<x4
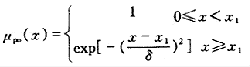
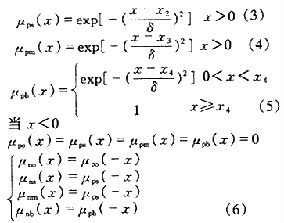
將偏差E經整型化處理變為離散整型變量xe后,選取如下的模糊變量![]() 來表示偏差xe的大小:
來表示偏差xe的大小:
{PB,PM,PS,PO,NO,NS,NM,NB}?
這些模糊變量的隸屬函數賦值μ?e如表2所示。
選擇如下的模糊變量![]() 來表示偏差變化量yce的大小:
來表示偏差變化量yce的大小:
{PB,PM,PS,O,NS,NM,NB}
偏差變化量CE的模糊變量![]() 的隸屬函數賦值μce如表3所示。
的隸屬函數賦值μce如表3所示。
與偏差和偏差變化的數據處理方法相同,將控制變量的變化量ΔU化為在[-7,+7]之間變化的離散整型變量zΔu,它的模糊變量![]() 的隸屬函數賦值μu如表4所示。
的隸屬函數賦值μu如表4所示。
| xe | ||||||||||||||
| -6 | -5 | -4 | -3 | -2 | -1 | -0 | +0 | +1 | +2 | +3 | +4 | +5 | +6 | |
| PB | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.1 | 0.4 | 0.8 | 1.0 |
| PM | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.2 | 0.7 | 1.0 | 0.7 | 0.2 |
| PS | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.3 | 0.8 | 1.0 | 0.5 | 0.1 | 0 | 0 |
| PO | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.0 | 0.6 | 0.1 | 0 | 0 | 0 | 0 |
| NO | 0 | 0 | 0 | 0 | 0.1 | 0.6 | 1.0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| NS | 0 | 0 | 0.1 | 0.5 | 1.0 | 0.8 | 0.3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| NM | 0.2 | 0.7 | 1.0 | 0.7 | 0.2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| NB | 1.0 | 0.8 | 0.4 | 0.1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
1.2 控制規則的建立
模糊控制規則很容易用計算機語言的條件語句來描述,本研究中生物電極脫氮法模糊控制規則的部分條件語句如表5所示,完整的模糊控制規則如表6所示。
| yce | |||||||||||||
| -6 | -5 | -4 | -3 | -2 | -1 | 0 | +1 | +2 | +3 | +4 | +5 | +6 | |
| PB | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.1 | 0.4 | 0.8 | 1.0 |
| PM | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.2 | 0.7 | 1.0 | 0.7 | 0.2 |
| PS | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.9 | 1.0 | 0.7 | 0.2 | 0 | 0 |
| O | 0 | 0 | 0 | 0 | 0 | 0.5 | 1.0 | 0.5 | 0 | 0 | 0 | 0 | 0 |
| NS | 0 | 0 | 0.2 | 0.7 | 1.0 | 0.9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| NM | 0.2 | 0.7 | 1.0 | 0.7 | 0.2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| NB | 1.0 | 0.8 | 0.4 | 0.1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Ζ△u | |||||||||||||||
| -7 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | +1 | +2 | +3 | +4 | +5 | +6 | +7 | |
| PB | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.1 | 0.4 | 0.8 | 1.0 |
| PM | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.2 | 0.7 | 1.0 | 0.7 | 0.2 | 0 |
| PS | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.4 | 1.0 | 0.8 | 0.4 | 0.1 | 0 | 0 | 0 |
| O | 0 | 0 | 0 | 0 | 0 | 0 | 0.2 | 1.0 | 0.2 | 0 | 0 | 0 | 0 | 0 | 0 |
| NS | 0 | 0 | 0 | 0.1 | 0.4 | 0.8 | 1.0 | 0.1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| NM | 0 | 0.2 | 0.7 | 1.0 | 0.7 | 0.2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| NB | 1.0 | 0.8 | 0.4 | 0.1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| if | e=NB | then | if | ce=not(PB or PM or PS | then | △u=PB | |
| or | if | e=NB | then | if | ce=PS | then | △u=PM |
| or | if | e=NB | then | if | ce=PM | then | △u=PS |
| or | if | e=NB | then | if | ce=PB | then | △u=O |
| or | if | e=NB | then | if | ce=(NH or NM or NS) | then | △u=PB |
| or | if | e=NB | then | if | ce=O | then | △u=PM |
| ... | ... | ... | |||||
| or | if | e=NB | then | if | ce=NB | then | △u=O |
| or | if | e=NB | then | if | ce=NM | then | △u=NS |
| or | if | e=NB | then | if | ce=NS | then | △u=NM |
| or | if | e=NB | then | △u=NB |
| ce | |||||||
| NB | NM | NS | O | PS | PM | PB | |
| NB | PB | PB | PB | PB | PM | PS | O |
| NM | PB | PB | PB | PM | PS | O | NS |
| NS | PB | PM | PM | PS | O | NS | NM |
| NO | PM | PM | PS | O | NS | NS | NM |
| PO | PM | PS | PS | O | NS | NM | NM |
| PS | PM | PS | O | NS | NM | NM | NB |
| PM | PS | O | NS | NM | NB | NB | NB |
| PB | O | NS | NM | NB | NB | NB | NB |
建立生物電極脫氮法模糊控制規則表的基本原則是:在適當考慮偏差變化模糊變量![]() 大小的前提下,當偏差大或較大時,以盡快消除偏差為主來選擇控制變化量;而當偏差較小時,注意防止超調和以被控制系統的穩定性為主來選擇控制變化量。
大小的前提下,當偏差大或較大時,以盡快消除偏差為主來選擇控制變化量;而當偏差較小時,注意防止超調和以被控制系統的穩定性為主來選擇控制變化量。
1.3 模糊控制器輸出變量的非模糊化
由表6可見,模糊控制器根據其控制規則輸出的是一個模糊量,這個模糊量不能直接控制被控系統,還必須經過非模糊化處理將其轉換成確定量。按表6確定的控制變量的模糊變量Δu都對應一個模糊子集(見表4),根據這個模糊子集將這個模糊變量進行非模糊化處理,使之轉變為被控系統能接受且確定的控制變量變化量,主要有兩種方法:一是選取該模糊子集中隸屬度最大的元素(即隸屬度最大時對應的坐標)作為控制變化量,即
![]()
式中z△u*——經非模糊化得到的規格化論域中的一個確定值,當得到多于一個解時,可以取其平均值
另一種方法是取模糊集合的重心坐標作為控制變量變化量非模糊化的值zΔu,其計算公式為:
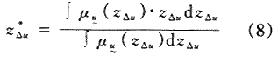
它也稱加權平均法,用離散數據的計算公式為:
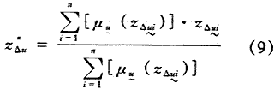
一般認為,第一種選取最大隸屬度方法簡單易行,但它只考慮隸屬度最大點的控制作用,利用信息量少,故多采用第二種方法。但是,單獨采用上述某一種方法并不能得到滿意的結果。例如,當偏差和偏差變化的模糊變量![]() 和
和![]() 都是NB或PB,得到的控制變量變化量的模糊變量
都是NB或PB,得到的控制變量變化量的模糊變量![]() 則為PB或NB時,顯然非模糊化處理時用加權平均法就不合適了。因此,本文在非模糊化處理時,將上述兩種方法結合起來,在應用模糊推理合成規則時,再參考
則為PB或NB時,顯然非模糊化處理時用加權平均法就不合適了。因此,本文在非模糊化處理時,將上述兩種方法結合起來,在應用模糊推理合成規則時,再參考![]() 和
和![]() 的各模糊子集的分布情況,經過適當調整,得到生物電極脫氮法的模糊控制表,見表7。
的各模糊子集的分布情況,經過適當調整,得到生物電極脫氮法的模糊控制表,見表7。
| xe | yce | ||||||||||||
| -6 | -5 | -4 | -3 | -2 | -1 | 0 | +1 | +2 | +3 | +4 | +5 | +6 | |
| -6 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 5 | 4 | 3 | 2 | 1 | 0 |
| -5 | 7 | 7 | 7 | 7 | 7 | 6 | 6 | 4 | 3 | 2 | 1 | 0 | 0 |
| -4 | 7 | 7 | 7 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 0 | -1 |
| -3 | 7 | 7 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 0 | -1 | -2 |
| -2 | 7 | 7 | 5 | 4 | 4 | 3 | 2 | 1 | 0 | 0 | -1 | -2 | -3 |
| -1 | 7 | 6 | 4 | 3 | 3 | 2 | 1 | 0 | 0 | -2 | -3 | -4 | -5 |
| -0 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 0 | -1 | -2 | -3 | -4 | -5 |
| +0 | 5 | 4 | 3 | 2 | 1 | 0 | 0 | -1 | -2 | -3 | -4 | -5 | -6 |
| +1 | 5 | 4 | 3 | 2 | 0 | 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 |
| +2 | 3 | 2 | 1 | 0 | 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -7 |
| +3 | 2 | 1 | 0 | 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -7 | -7 |
| +4 | 1 | 0 | 0 | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -7 | -7 | -7 |
| +5 | 0 | 0 | -1 | -2 | -3 | -4 | -6 | -6 | -7 | -7 | -7 | -7 | -7 |
| +6 | 0 | -1 | -2 | -3 | -4 | -5 | -7 | -7 | -7 | -7 | -7 | -7 | -7 |
表7也稱查詢表,它可存放在計算機內存中(除非需要修改時)。在實時控制中,根據離散整數化處理后的偏差與偏差變化值,可以直接從查詢表中找到相應的控制變量變化量zΔu。但是,這個無量綱控制變量變化量還必須轉換到被控制對象所能接受的控制變量變化量的基本論域中去,如式(10)所示。
ΔU=KuzΔu (10)
式中Ku——比例因子,表示將控制變化量zΔu從論域[-7,+7]轉換為有確定值的控制變量變化量ΔU的相關系數根據式(6)和式(7)可將ΔU變成電流密度的變化量或(和)有機物投加量的變化量。
2 在線模糊控制的計算機算法
首先要確定采樣周期,采樣周期越小,越接近連續實時控制。如果處理水中Noff可以連續測定或傳感器測定的滯后時間很短,并且執行機構的響應過程十分迅速,采樣周期可取5~30s;否則可取30~60s。在線模糊控制的優點是采樣周期較長時,也能使被控制系統較迅速地趨向平穩。
本系統的在線模糊控制計算機程序框圖如圖2所示。偏差E、偏差變化量CE、控制變量變化量ΔU的基本論域、控制變量的初值U0和最大電流密度Imax等,都應根據被控系統的運行數據與經驗來設置與修正。其主要算法如下:
① 將傳感器的檢測結果Noffi輸入計算機,得出偏差Ei及其變化量CEi,并將其分別轉換到相應的整數論域Xei和Ycei中。
② 將Xei和Ycei進行模糊化處理,得到相應的模糊集合![]() 和
和![]() ,根據模糊控制理論,按模糊推理合成規則,計算出控制變量變化量
,根據模糊控制理論,按模糊推理合成規則,計算出控制變量變化量![]() 。
。
③ 對![]() 進行非模糊化處理后轉化為離散整數表示的控制變量變化量zΔui,再將zΔui轉換到其基本論域中,得到控制變量變化量Δui。
進行非模糊化處理后轉化為離散整數表示的控制變量變化量zΔui,再將zΔui轉換到其基本論域中,得到控制變量變化量Δui。
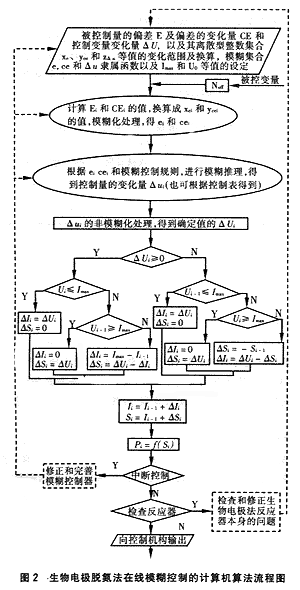
④ 將ΔUi換算成電流密度的變化量ΔIi或(和)有機物投加量的變化量ΔSi;再根據上一采樣周期的控制變量,計算出本采樣周期的控制變量Ii和Si。必要時根據有機物投加量Si計算出Pi的投加量。
⑤ 然后用得到的新的控制變量通過控制執行機構對生物電極法反應器進行在線控制。繼續進行下一采樣周期的控制。
3 結論
綜上所述,本研究的在線模糊控制系統具有如下優點:?
① 構造簡單、可行性好?
首先是由于生物電極法的被控制變量只選擇處理水的硝酸態氮濃度Noff,即只需一個在線NOx--N傳感器或監視器(不能連續監測也可),而不必監測進水水質水量以及其它變量和變化速率;其次是作為輸入控制變量的電流密度(通過電壓控制)和有機物投加量也很容易做到定量控制,使系統的可控性好。
② 可靠性與穩定性好
由于生物電極法的目的就是脫氮,因此,本控制系統以處理水中的Noff與處理水標準Ns的偏差和該偏差的變化這兩者作為模糊控制的輸入變量。這兩個變量不僅直接給出了處理水水質,而且還間接地反映出進水硝酸態氮的負荷量及其變化速率。所以通過模糊控制器的判斷與計算輸出的控制變量變化量ΔUi的針對性很強,使它既盡快消除處理水水質的偏差,又考慮到了進水水質水量變化對處理水水質的影響。具有控制響應的滯后性小,保持被控系統運行穩定性好的優點。
③ 適用進水硝酸態氮負荷變化范圍廣
由圖2可見,如果進水中的Nin濃度較低或(和)進水流量小,只控制生物電極法反應器的電流密度即可,不須投加有機物作供氫體;如果進水硝酸態氮的負荷較高,則在電流密度達到Imax時,再根據ΔUi的值控制投加有機物。因此本控制系統能在進水負荷變化很大的范圍內,使出水達標,具有適應性強的特點。
④ 有利于避免過量地投加有機物并盡可能節省運行費用?
一是在低進水NOx--N負荷時,可控制不投加有機物。二是始終將電流密度控制在高效率范圍內。三是根據具體情況可以合理地設置處理水標準NS(比如NS=5~9mg/L),在NS不接近于零并且稍高時,脫氮速度也較快,且有機物的投加可以小于化學計量的理論需要量[4]。這不僅可以避免處理水中殘留有機物,而且也能提高電解氫的利用率。四是本控制系統的原則是控制處理水水質Noff剛好達到處理水標準NS。上述四個控制策略都有利于避免處理水中含有機物、保持較高的脫氮速率和盡可能降低運行費用。
⑤ 可以不斷完善本模糊控制器
根據在實際運行中的數據、經驗、生物膜增長情況和進水類型等,可以完善與修正模糊控制器(包括模糊與非模糊化處理、模糊關系、模糊決策等),不斷提高其控制品質。
應當指出,本研究提出的在線模糊控制系統能夠正常運行,或者說充分發揮上述優點,應依賴于生物電極脫氮反應器的正常運行。例如,反應器的電極上應附著脫氮活性較好的生物膜,以及在反應器的設計和運行時應避免進水硝酸態氮的量超負荷。這是因為如果電極上沒有足夠的脫氮菌或當進水硝酸態氮的量超過反應器能承受的負荷時,無論采用什么控制方法都是難以奏效的。
在模糊控制器軟件的具體設計時,還需要有處理水硝酸態氮的偏差及偏差變化量與改變電流密度的量或投加有機物的量之間關系的更詳盡的資料。此外,P投加量與有機物投加量之間的定量關系如何等,都需要根據生物電極脫氮法處理不同的硝酸態氮污染水的運行數據和經驗來確定。
參考文獻
1 彭永臻,王淑瑩,周利等.生物電極脫氮工藝的在線模糊控制研究(一).中國給水排水,1999;15(2):5~9
2 李士勇等.模糊控制和智能控制理論與應用.哈爾濱:哈爾濱工業大學出版社,1990
3 菅野道夫.フアヅイ制御.日刊工業新聞社,1988
4 黑田正和等.バイオエレクト口法による硝酸污染水の脫窒特性とその高速處理に關する檢討.水環境學會志,1994;17(10):623
國家自然科學基金資助項目
作者簡介:彭永臻 教授 工學博士 博士生導師
通訊處:150008 哈爾濱建筑大學新區607信箱
(收稿日期 1998-09-06)
論文搜索
發表時間 至
月熱點論文
論文投稿
很多時候您的文章總是無緣變成鉛字。研究做到關鍵時,試驗有了起色時,是不是想和同行探討一下,工作中有了心得,您是不是很想與人分享,那么不要只是默默工作了,寫下來吧!投稿時,請以附件形式發至 paper@h2o-china.com ,請注明論文投稿。一旦采用,我們會為您增加100枚金幣。








