景有海¹，金同軌¹，范瑾初²
（1.西安建筑科技大學(xué) 環(huán)境與市政工程學(xué)院，陜西 西安 710055；2.同濟(jì)大學(xué) 環(huán)境科學(xué)與工程學(xué)院，上海 200092）

　　摘要：通過將粒狀材料組成的濾床抽象為由無數(shù)條毛細(xì)管道組成的管束，將過濾過程描述為水流在毛細(xì)管道中流動(dòng)時(shí)的管壁吸附過程，從而推導(dǎo)出了均質(zhì)濾料過濾過程的濁質(zhì)去除數(shù)學(xué)模型。
　　關(guān)鍵詞：均質(zhì)濾料；過濾過程；毛細(xì)管模型；過濾方程
　　中圖分類號(hào)：TU991.24
　　文獻(xiàn)標(biāo)識(shí)碼：A
　　文章編號(hào)：1000-4602(2000)06-0001-04

Capillaries Model for Turbidity Removal in Filtration Process with Uniform Media

JING You hai¹，JIN Tong gui¹，F(xiàn)AN Jin chu²
(1.School of Environ. and Munic. Eng., Xi‘a(chǎn)n Univ. of Architec. and Tech., Xi’an 710055,China; 2.School of Environ.Sci.and Eng.,Tongji Univ.,Shanghai 200092, China)

? Abstract：based on simulating the granular filter bed as tubes formed by numerous cylindrical capillaries, this paper described filtration tube wall adsorption process when water was flowing in capillaries. results, a mathematical model of turbidity removal with uniform media deduced.?
　　Keywords: uniform media;filtration;capillaries model;filtration equation

　　基金項(xiàng)目： 國家自然科學(xué)基金資助項(xiàng)目(59778022)

　　1.均質(zhì)濾料過濾過程的毛細(xì)管模型

　　由粒狀材料組成的濾床，內(nèi)部有無數(shù)孔隙通道。水流通過濾層的過濾過程，就是水流在濾床孔隙內(nèi)的流動(dòng)過程。因此，可將濾床看成是有無數(shù)條毛細(xì)管道組成的管束，過濾過程就是水流在這些毛細(xì)管道中的流動(dòng)過程。為了使水流在毛細(xì)管道中的過濾條件與實(shí)際濾床中的過濾條件相同，必須具備以下兩個(gè)條件：
　　① 毛細(xì)管道的總空間應(yīng)與濾床的孔隙相同；
　　② 毛細(xì)管道的總表面積應(yīng)與濾料的表面積相同。
　　假設(shè)濾池面積為F(m²)，濾床深度為L(m)，濾料的孔隙率為ε(m³孔隙/m³濾料)，濾料的比表面積為f(m²表面/m³濾料)；并假設(shè)單位面積濾池?fù)碛忻?xì)管數(shù)量為n(根/m²濾池)，毛細(xì)管的管徑為d_m(m)。因此，根據(jù)上述兩條原則，將均質(zhì)濾料濾床描述為毛細(xì)管模型時(shí)，必須滿足下列兩個(gè)等式：

　　ε＝n·πd_m²/4 　　　　　　　　　(1)
　　f＝n·πd_m　　　　　　　　　　　 (2)

　　對(duì)于非球形級(jí)配濾料，其比表面積可表示為：

　　f=6α(1-ε)/d_e　　　　　　　　　　(3)

　　式中　α——濾料的表面形狀系數(shù)
　　　　　d_e——濾料的當(dāng)量直徑，m

　　聯(lián)解式（1）和式（2），并將式(3)代入可得：

　　dm=2εd_e/(3α(1-ε)) 　　　　　(4)
　　n=9α²(1-ε)²/πεd_e 　　　　　(5)

　　此即為筆者將濾池抽象為毛細(xì)管模型時(shí)的毛細(xì)管管徑和單位面積濾池?fù)碛忻?xì)管數(shù)量的計(jì)算公式。

　　2 過濾過程的濁質(zhì)去除計(jì)算模型

　　取濾層中某一毛細(xì)管作為考查對(duì)象，在濾層深度z處取斷面1，并在深度z+dz處取斷面2，如圖1所示。

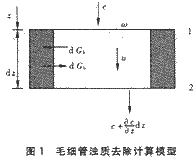
　　假設(shè)在時(shí)刻t,斷面1處的濁質(zhì)濃度為c，過流斷面面積為ω，沉積在毛細(xì)管壁單位管長上的濁質(zhì)體積量為σd(m³濁質(zhì)/m管長），濾層的濁質(zhì)比沉積量為σd(m³濁質(zhì)m³濾料），則有：

　　σd=σ/n （6）

　　斷面2處的濁質(zhì)濃度為： ，經(jīng)過dt時(shí)段后，dz長度毛細(xì)管壁上的濁質(zhì)增加量為：

　　

　　水中濁質(zhì)因被毛細(xì)管壁吸附后，其管壁附近濁質(zhì)濃度降低，使得毛細(xì)管中心濁質(zhì)與管壁附近出現(xiàn)濃度梯度。在濃度梯度的推動(dòng)下，管中心濁質(zhì)向管壁擴(kuò)散，這種擴(kuò)散包括面朗運(yùn)動(dòng)擴(kuò)散和水力擴(kuò)散。

　　

　　式中　D——濁質(zhì)的擴(kuò)散系數(shù)，m²/s
　　　　　rm——毛細(xì)管壁吸附濁質(zhì)后的孔道半徑，m
　　因此，經(jīng)dt時(shí)段的擴(kuò)散量即沉積量為：

　　

　　沉積在毛細(xì)管壁上的濁質(zhì)，因水流的剪切力而被剝落下來，其剝離速率可認(rèn)為與水流的剪切力和毛細(xì)管道的堵塞率成正比，即：

　　

　　式中 B——濁質(zhì)的剝離系數(shù)，m3/(N.s），與濾料的表面特性以及水中濁質(zhì)顆粒的表面特性即混凝特性有關(guān)。混凝效果好，B值小，否則B值大。采用高分子混凝劑時(shí)，其B值就遠(yuǎn)小于采用硫酸鋁作混凝劑時(shí)的B值
　　　　τ——水流的剪切應(yīng)力，N/m2
　　　　μ——水的動(dòng)力粘性系數(shù)，Pa.s
　　則其剝離量為：

　　

　　式（12）即為本文作者推導(dǎo)出的均質(zhì)濾料過濾過程的濾層堵塞方程式，式中濾速v的單位為m/s。
　　在濾層中取一毛細(xì)管作為考查對(duì)象，如圖2所示。由表層算起，毛細(xì)管長管為z，進(jìn)入毛細(xì)管的濁質(zhì)濃度為c0，從毛細(xì)管流出的濁質(zhì)濃度為c。過濾從時(shí)間0開始，經(jīng)過時(shí)段t過濾后，毛細(xì)管單位長度上的濁質(zhì)吸附量σd，根據(jù)物料平衡有：

　　

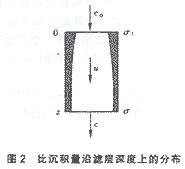
　　式（14）即為本文作者推導(dǎo)出的均質(zhì)濾料過濾過程的連續(xù)性方程。式中c為過濾流體中的濁質(zhì)何種濃度，其單位為（m³固體/m³液體）。顯然，c的最大值為1。當(dāng)c=1時(shí)，表示過濾介質(zhì)變?yōu)楣腆w。在一般的流體過濾過程中，其注質(zhì)濃度c＜＜1，則上式可簡化為：

　　

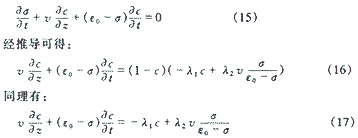
　　式（16）和式（17）即為本文作者推導(dǎo)出的均質(zhì)濾料過濾過程的毛細(xì)管去除濁質(zhì)計(jì)算模型，即過濾方程。由式（12）和式（17）可以看出：當(dāng)進(jìn)水濁質(zhì)濃度c=0、比沉積量σ≠0時(shí)，濁質(zhì)的去除速率為正值，而比沉積量的沉積速率為負(fù)值。這說明水中濁質(zhì)濃度增加，而比沉積量減小，它正好描述了反沖洗時(shí)的濾層清潔過程。因此式（12）、（15）和（17）不僅是過濾方程，同時(shí)也是濾層在不擾動(dòng)情況下的反沖洗方程，這正好說明反沖洗過程是過濾過程的逆過程。

　　3 過濾方程式的簡化分析

　　方程（12）、（15）和（17）中，σ和c均為濾層深度z和過濾時(shí)間t的函數(shù)，即：

　　σ=σ（z，t) （18）
　　c=c(z,t） （19）

　　顯然，上述方程為二元二次函數(shù)一階非線性方程組，目前還難以求得其精確的解析解。現(xiàn)對(duì)其進(jìn)行簡化分析和近似解答，更精確的解答要通過數(shù)值分析來求得。
　　3.1 濾層中的最大比沉積量
　　對(duì)于濾層堵塞方程式（12），當(dāng)濾層截留濁質(zhì)達(dá)到飽和時(shí)，有：

　　

　　3.2 濾層失去除濁能力時(shí)所需過濾時(shí)間
　　對(duì)于濾層表層，當(dāng)z=0時(shí)，有c=c0=常數(shù)，此時(shí)，濾層堵塞方程（12）變?yōu)椋?

　　dσ_i/dt=λ₁c₀-λ₂[σ_i/(ε₀-σ_i)]υ 　　（25）

　　上式中，σ_i為z=0時(shí)的濾層比截污量。對(duì)止式積分并設(shè)過濾是從清潔濾層開始，當(dāng)t=0時(shí)，σ_i=0，則有：

　　t=（λ₂υε₀/φ）ln[λ₁υε₀/（λ₁υε₀-φσ_i）+σ_i/φ （26）

　　當(dāng)濾層即將失去除濁能力時(shí)，有σ_i→σ_max=λ₁υε₀/φ，此時(shí)所需要的過濾時(shí)間為：

　　

　　也就是說，在有限的過濾時(shí)間內(nèi)，理論上濾層難以達(dá)到完全飽和，這在過濾試驗(yàn)中已基本得到證實(shí)。因此，在實(shí)際應(yīng)用中，當(dāng)σ=95%σmax時(shí)，即可認(rèn)為濾層已達(dá)到飽和狀態(tài)。此時(shí)所需要的過濾時(shí)間為：

　　

　　3.3 濾層沿深度方向的比沉積量分布規(guī)律
　　由濾層堵塞方程，因σ/（ε₀-σ）=u，得到：

　　

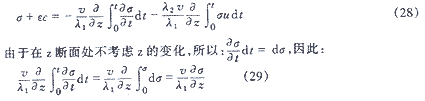
　　對(duì)于式（28）右邊第二項(xiàng)，由于udt=dz，且有當(dāng)t=0時(shí)z=z當(dāng)t=t時(shí)z=z’，其z’為假設(shè)毛細(xì)管為無限長時(shí)，經(jīng)過t時(shí)間段后，流體沿毛細(xì)管流行的距離，因此有

　　

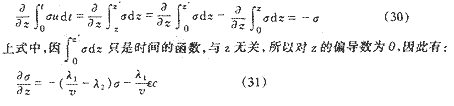
　　式（31）即為比沉積量沿濾層深度方向上的分布規(guī)律。
　　由式（12）和式（31）可得：

　　

　　式中σi為濾層表層z=0處的比沉積量，它滿足方程（26）。由此可見，σ是過濾時(shí)間t和濾層深度z的函數(shù)。
　　由式（33）可以看出，在過濾過程中，濾層中的比沉積量沿深度方向近似按負(fù)指數(shù)規(guī)律衰減。提高濾速，則比沉積量衰減率減小，濁質(zhì)向?yàn)V層深處穿透，比沉積量在濾層中的分布趨于均勻。混凝效果提高，λ₂減小，比沉積量衰減率增大，表明濁質(zhì)較易被表層截留。
　　由式(31)可以看出， 不可能為0(除非λ₁＝λ₂＝0)。因此，嚴(yán)格講濾層中不可能出現(xiàn)飽和階段。否則，從函數(shù)連續(xù)性角度考慮，比沉積量沿深度方向的變化必然出現(xiàn)拐點(diǎn)。但因其分布近似于負(fù)指數(shù)規(guī)律，不可能有拐點(diǎn)。另一方面，假如濾層中有飽和層出現(xiàn)，那么該濾層中將不會(huì)再有濁質(zhì)截留，該段濾層的水頭損失也將不會(huì)再隨過濾時(shí)間的延長而增大。但在過濾試驗(yàn)中并未發(fā)現(xiàn)這樣的階段出現(xiàn)。因此可以說，在過濾過程中，濾層中不可能有飽和階段出現(xiàn)。

　　4 結(jié)論

　　① 將均質(zhì)濾料濾池描述為毛細(xì)管模型有助于簡化過濾過程的分析，其結(jié)論仍然可用。
　　② 在有限的過濾時(shí)間內(nèi)，嚴(yán)格講，濾層中不可能出現(xiàn)飽和階段。
　　③ 濾層中的比沉積量近似按負(fù)指數(shù)規(guī)律分布。

參考文獻(xiàn)：
［1］許保玖，安鼎年.給水處理理論與設(shè)計(jì)［M］.北京：中國建筑工業(yè)出版社，1992.
［2］嚴(yán)熙世，范瑾初.給水工程［M］.北京：中國建筑工業(yè)出版社，1995.
［3］Ю·M·康士坦丁諾夫.水力學(xué)［M］.鐘用升譯.江西高校出版社，1990.

---

作者簡介：景有海(1962-)，男，陜西隴縣人，西安建筑科技大學(xué)副教授，碩士，主要從事水處理技術(shù)方面的教學(xué)和科研工作。
電話：(029)5234941
收稿日期：2000-01-23