樊建軍，劉金香，袁華山
(南華大學建筑工程與資源環境學院，湖南衡陽421001)

　　摘　要：為克服明渠水力計算中試算法帶有盲目性、計算工作量大和圖解法使用不便、精度較差的缺陷，在對明渠水力計算公式進行充分剖析的基礎上，給出了相應的迭代公式，并從數學上證明了迭代公式的收斂性。公式用于工程設計計算具有速度快、精度高的優點，效果令人滿意。
　　關鍵詞：迭代法；明渠；水力計算
　　中圖分類號：TU991.32
　　文獻標識碼：C
　　文章編號：1000-4602(2001)06-0043-02

1　基本公式與迭代公式

　　明渠均勻流的基本公式為：

　　
　　式中　Q——流量
　　　　　i——渠道底坡
　　　　　n——粗糙系數
　　　　　m——邊坡系數
　　　　　b——渠底寬度
　　　　　h——水深
　　對基本公式加以改造，可得求解b或h的迭代公式：

　　

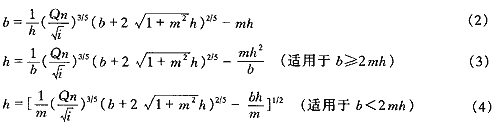
　　明渠水流處于臨界流狀態時，各參數滿足以下關系：

　　　　　　αQ²／g＝(b+mhk)³h_k／b+2mh_k　　　　　　　　　(5)
　　式中　α——動能修正系數，通常取α＝1
　　　　　g——重力加速度
　　　　　hk——臨界水深

　　對式(5)進行改造，可得計算臨界水深的迭代公式：
　　
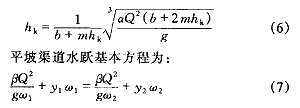
　　式中　β——動量修正系數，通常取β＝1
　　　　　ω——過水斷面面積，ω＝(b+mh)h
　　　　　y——過水斷面形心水深，y＝3bh+2mh²／6(b+mh)
　　令θ(h)＝βQ²／gω+yω，用h′與h″分別代表躍前水深與躍后水深，由水躍基本方程可導出以下迭代公式：
　　

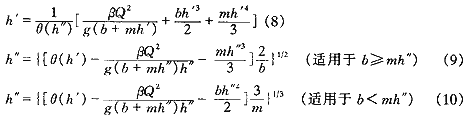
2　收斂性證明

　　根據迭代理論，假設方程f(x)＝0的一個根為a，若把f(x)＝0變形為x＝φ(x)，則迭代形式xn+1＝φ(xn)收斂于a的條件是，如果在a的某一鄰域｜x-a｜＜δ內，｜φ′(x)｜＜1，那么以該鄰域內任一點為初值的迭代都收斂于a。
　　下面以迭代式(2)為例，證明其收斂性，其他迭代式都可用同樣方法得到證明。
　　

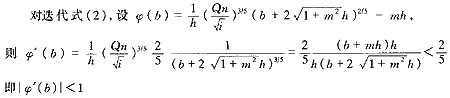
3　迭代初值的確定及實例計算

　　雖然迭代式(2)、(3)、(4)、(6)、(8)、(9)、(10)對公式適用范圍內的任意初值均收斂，但初值選取是否恰當對迭代計算工作量有一定影響。通過深入分析迭代公式各參數間的關系，建議對迭代式(2)、(3)、(4)、(6)均取初值為零，對迭代式(8)、(9)、(10)則分別取初值如下：
　　

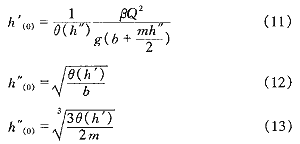
　　實例計算：
　　例1，有一梯形渠道，采用小片石干砌護面(n＝0.02)，設計流量Q＝10m3/s，m＝1.5，i＝0.003，要求水深h＝1.5 m，試確定渠底寬度b。
　　解：用迭代式(2)計算，取初值b(0)＝0，可求得b(1)＝0.60，b(2)＝0.72，b(3)＝0.75，b(4)＝0.75。
取渠底寬度為0.75 m。
　　例2，有一梯形渠道，用大塊石干砌護面(n＝0.02)，已知b＝7 m，m＝1.5，i＝0.001 5，需要通過流量Q＝18 m3/s，試確定渠道的正常水深h。
　　解：初估水深＜2 m，則b＞2 mh，可用迭代式(3)計算，取初值h(0)＝0，代入式(3)可求得h(1)＝1.19，h(2)＝1.13，h(3)＝1.15，h(4)＝1.14。
　　取正常水深為1.14 m。
　　例3，有一梯形斷面小河，b＝10 m，m＝1.5，Q＝30m³/s，試確定臨界水深。
　　解：用迭代式(6)計算，取初值hk(0)＝0，可求得hk(1)＝0.972，hk(2)＝0.924，hk(3)＝0.926，hk(4)＝0.926。
　　取hk＝0.926 m。
　　例4，某梯形渠道，b＝7 m，m＝1，Q＝54.3m³/s，渠中有水躍發生，已知h′＝0.8 m，試確定h″。
　　解：初估h″＜7 m，則b＞mh″，可用迭代式(9)計算。
　　　

4　結語

　　實例計算表明，文中給出的迭代方法相對于目前采用的試算法和圖解法而言，既減少了計算工作量，又提高了計算精度，不失為工程設計計算的好方法。
　　雖然求解正常水深和躍后水深的迭代公式均有兩個，但根據具體問題和計算者的實踐經驗，很容易確定采用哪一個迭代式，即使起初無法判斷，也只需經過一次迭代后就能作出正確判斷，使用也是方便的。
　　因迭代計算是簡單的重復，經常從事明渠水力計算的工作人員可編制迭代計算程序，采用計算機運算，一勞永逸。

參考文獻：

　　［1］清華大學水力學教研室編.水力學［M］.北京：人民教育出版社，1980.
　　［2］成都科學技術大學水力學教研室編.水力學(上冊)［M］.北京：人民教育出版社，1979.
　　［3］武漢大學，山東大學編.計算方法［M］.北京：人民教育出版社，1979.

---

　　電　話：(0734)8282020
　　收稿日期：2000-11-21