任伯幟1，沈良峰1，許仕榮2，王濤2，謝社平2?
( 1.湘潭工學院土木工程系，湖南湘潭411201； 2.湖南大學土木工程學院，湖南長沙410082)

　　摘　要： 在修編長沙市暴雨強度公式的實踐中，通過對現有各種求解城市暴雨強度公式參數的計算方法分析，提出應用帶因子—迭代法求解。結果表明，該法不但較好地解決了非線性方程線性化時易出現的病態問題，而且放寬了迭代初始值的選擇范圍，迭代收斂性較好、求解過程穩定、擬合精度較高，實用可行。
　　關鍵詞：城市排水；暴雨強度公式；帶因子—迭代法；非線性方程；參數估計
　　中圖分類號：TU823.6
　　文獻標識碼：C
　　文章編號：1000-4602(2002)02-0063-03

1 模型的建立

　　曲線擬合或科學試驗中常見下列非線性方程組：?
　　fj(xj，yj，zj，…，ai)=0(i=1,2,3，…，m;j=1,2 ,3,…，N)　　　(1)?
　　其中fj(j=1,2,3,…，N)是m個參變量ai(i=1,2,3,…，m)的非線性函數。(xj,yj,zj)是通過N次試驗觀測所得的N組已知數據。在求解式(1)非線性方程組的參數ai時，常化為多元函數的極小值問題，即求與之等價的目標函數的極小值問題，從而確定參數ai：?

　　用矩陣與向量記號表示：X=［x1,x?2,x?3,…，xN］^T，Y=［y1,y2,y3,…，yN］^T?
　　　　　　　　　　　　　Z=［z1,z2,z3,…，zN］^T，A=［a1,a2,a3,…，am］^T
　　則有：F(X，Y，Z，A)=［f1(X,Y,Z,A),f2(X,Y,Z,A),f3(X,Y,Z,A),…，fN(X,Y,Z,A )］^T
　　則式(1)可改成：?
　　　　　V(X,Y,Z,A)=F(X,Y,Z,A)T?
　　　　　F(X,Y,Z,A)=‖F(X，Y，Z，A)‖²　　(3)?
　　為使式(2)、(3)有極小值，則需：

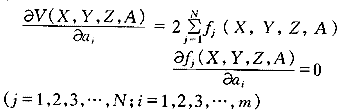
　　即有：V(X,Y,Z,A)=2DF(X,Y,Z,A)^T　　F(X,Y,Z,A)=0　　(4)

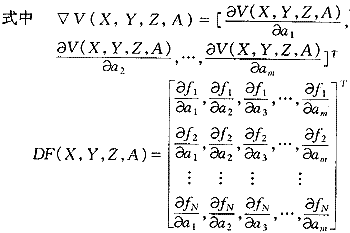
　　因F(X，Y，Z，A)是關于A的非線性函數，為此方程(4)是一個非線性方程組，一般難于直接求解，常采用逐次線性化處理。即設A0為解的初始近似值，ΔA為精確值與初始值之差，則有：A=A0+ΔA，將F(X，Y，Z，A)在A0附近Taylor展開，并略去ΔA的二次及二次以上各項得：?
　　F(X，Y，Z，A)=F(X,Y,Z,A0)+DF(X,Y,Z,A0)ΔA　　　　　(5)?
　　將式(5)代入式(3)，再由式(4)得：?
　　　　DF(X，Y，Z，A₀)T DF(X，Y，Z，A0) ?
　　　　ΔA+DF(X，Y，Z，A0)TF(X,Y, Z,A0)=0　　　　　　　(6)?
　　由于F(X，Y，Z，A)復雜的非線性，由Taylor展開線性化后得到的線性方程組易出現病態問題，給式(6)求解帶來困難，為此引進阻尼因子u，從而增大［DF(X，Y，Z，A₀)TDF(X， Y，Z，A₀)］的主對角元素的值，則式(6)變為：?
　　DF(X，Y，Z，A₀)TDF(X，Y，Z，A₀)+uIm］ΔA+DF(X,Y,Z,A₀)T F(X，Y，Z，A₀)=0　　(7)?
　　式中Im——m×m階單位矩陣?

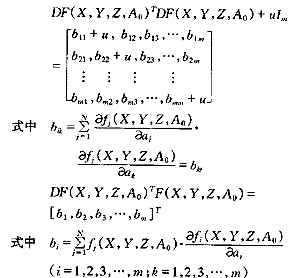
　　在迭代求解式(7)時，為放寬對初始值A0的選擇，使迭代收斂或加速收斂，引入步長因子ω，即解方程組(7)得出的ΔA，不是直接由A=A₀+ΔA計算第一次近似值，而是把ΔA作為尋查方向，即改為：
A=A?0+ωΔA　　　　　　(8)?
　　其中步長因子ω的選擇應滿足：?
V(X，Y，Z，A?0+ωΔA)＜V(X，Y，Z，A?0)　　　　　(9)?
　　則由式(7)、(8)、(9)及求解參數的精度要求(max[DD(][]l≤i≤m[DD)]｜a_i-a_i⁽⁰⁾｜=max｜ΔA｜≤ε，其中ε為求解精度)構成了帶因子—迭代法求解參數的數學模型。?

2　參數的求解

　　將i—t—p關系數據表中不同歷時t和不同重現期p對應的不同雨強i組成N組(ij,tj,pj )已知數據組(j=1,2,3,…，N；N=9個歷時×11個重現期=99)，則將城市暴雨強度公式變形得下列方程組：?

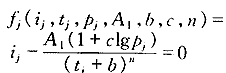
　　即：fj(ij,tj,pj,A1,b,c,n)=0(j=1,2,3,…，N)　　　　(10)?
　　式(10)中函數fj是關于4個參數(A1，b,c,n)的非線性函數，(ij,tj,pj)為N組已知數組。對函數fj中4個參數分別求導得：?

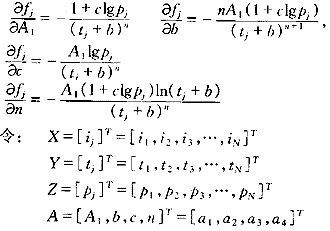
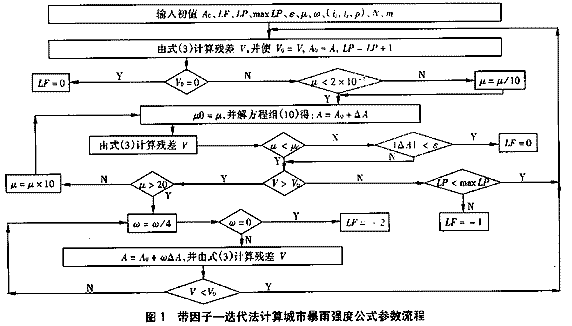
　　選擇迭代初值A0，由帶因子—迭代求參數模型按圖1進行迭代求解。當max｜ΔA｜≤ε時，則輸出待求參數A1、b、c、n。?
ε取值范圍一般為10^-3～10^-5；μ初值賦為0.01；ω初值賦為1；已知數 據組總數N=99；m=4；迭代次數LP初值賦為零；輸出參數LF=0表示計算成功并輸出參數，LF= -1表示迭代次數大于假定的maxLP時仍未收斂，可再放大maxLP進行迭代，LF=-2表 示u=100、ω=0，無法迭代下去(可能是因為精度要求太高)，改變精度要求即可繼續迭代。

3　應用實例

　　湖南省長沙市有連續25年(1974年—1998年)的雨量資料，每場暴雨取5、10、15、20、30、4 5、60、90、120min9個歷時段的最大降雨強度，每年各歷時取6個雨強最大值；不分年次先后按文獻^［6］的從大到小排序，選取其中4倍年份數的前面樣本作為統計的基礎資料，按文獻^［6］的計算方法得出長沙市的i—t—p關系數據，在此基礎上推求暴雨公式參數。
　　通過各種方法的應用程序計算得出的長沙市暴雨強度公式參數結果對比見表1。 表1　不同方法對長沙市暴雨強度公式參數的計算結果對比 計 算 方法 暴雨強度公式參數 V A₁ b c n CRE編制法 11.511 12.643 0.385 0.654 0.3071 單純加速法 11.782 12.730 0.389 0.665 0.2954 高斯—牛頓法 12.05 12.935 0.397 0.676 0.2641 迭代法 12.483 13.012 0.403 0.680 0.2336 麥夸爾特法 12.674 13.263 0.406 0.684 0.2053 帶因子—迭代法 12.877 13.275 0.410 0.685 0.1459

　　從表1可知，在相同的i—t—p關系數據表及比較條件下，用帶因子—迭代法推求城市暴雨強度公式參數優于其他方法，此法推求的長沙市暴雨強度公式為：?
?　i=[12.877(1+0.410 lgp)］/［(t+13.275)0.685］

4 結語

　　應用帶因子—迭代法推求城市暴雨強度公式參數的結果表明該法是合理可行的，它具有如下特點：?
　　①較好地克服了非線性方程線性化時易出現的病態問題，使迭代求解過程穩定；?
　　②較好地解決了現有各種方法中迭代初始值選擇的局限性，放寬了初始值的選擇范圍，且能做到迭代收斂或加速收斂；?
　　③應用實例表明該法優于現有各種方法，且精度滿足現行規范的要求。

參考文獻：

　　［1］GB 14—87，室外排水工程設計規范［S］.
　　［2］王世剛.城市暴雨公式參數優化計算程序［J］.中國給水排水，1987，3(4) ：50-52.
　　［3］張字賢.用高斯—迭代法求解暴雨強度公式參數［J］.河海大學學報，1995，23(5)：106-11 1.
　　［4］趙建國.迭代法求解暴雨強度公式參數［J］.給水排水，1997，23(12)：9- 12.
　　［5］李樹平，劉遂慶，黃延林.用麥夸爾特法推求暴雨強度公式參數［J］.給水排水，1999，25( 2)：26-28.
　　［6］任伯幟，許仕榮，王濤.皮爾遜—Ⅲ型分布統計參數的確定［J］.中國給水排水，2001，17( 1)：40-42.

　　電　話：(0732)8290041?
　　收稿日期：2001-06-31